谈谈热的动力和适合开发这种动力的机器(1824)
"论火的动力"
二〇二二 十二月
Sadi Carnot 萨迪·卡诺(法)/著 | K/译
序 - K
尼古拉·萨迪·卡诺(后简称“萨迪”),1796年出生于巴黎的小卢森堡宫(法国参议院),二十八岁完成《论热的动力》,热机循环的奠基人。萨迪·卡诺的父亲拉扎尔·卡诺是法国著名政治家和数学家,曾辅佐拿破仑组建了法兰西革命军,任后勤部长,被称为“胜利组织者”,是法兰西革命军重要的成功要素之一。拉扎尔·卡诺后任法兰西战争部长,法兰西共和国国防部长。后期因拿破仑的政治失势,萨迪的父亲拉扎尔流亡德国,萨迪本人也因此遭受社会排挤,颠沛流离,在孤独和霍乱疫情中死于一个不为人知的私人庇护所,终年三十六岁。出于当时法国的防疫需求,他死后的随身物品和记录都被烧毁。
萨迪·卡诺对热和动力机的研究启发了开尔文、克劳修斯等物理学家对热量的开创性研究。萨迪的传奇一生,大量细节不为人知,1824年6月12日,萨迪发表了《论热的动力》,但他的研究工作长时间因为战争、社会动荡和霍乱疫情被埋没,但在热力学研究最突飞猛进的后几十年间,英国的威廉·汤姆森(开尔文勋爵,绝对温标的单位K)、德国的克劳修斯(熵的提出者)都曾间接研究过卡诺著作中的重要内容。这几位热力学定律的奠基人不约而同地从萨迪·卡诺发现热力做功的秘密中得到了启发。萨迪发表的这本《论热的动力》在他活着和死后都从未在科学界引起震动,但他依然是发现热机循环规律的第一人,现在以他姓氏命名的“卡诺循环”遍布世界上任何一种语言的任何一本热力学教材。通过教科书能迅速获取严谨的科学结论,但如果永远只了解结论,而完全忽视科学发现的过程,对心智甚至有害。科学诞生于怀疑和实验,好奇与思考,直觉和感受,逻辑和想像。科学是对不合理事物的祛魅与抵抗。
萨迪的发现不是完美的,论文中的“热质说”也早已被现代热力学的“分子热运动”所取代。但科学本来就不完美,创造性的科学发现更不可能完美,重要发现在创造初期经常漏洞百出。但伟大发现之伟大,在于它们用并不绝对完美的论证,邀请所有人都加入这场重要的探索中,伟大的论述可以激发了更多伟大的思索,让谬误变得无比接近真理。这也是卡诺这部作品对热机和现代热力学的意义。他这部著作中展现的科学自信和敏锐观察,只有直接阅读原著才能体会到。这篇著作没有太多数学内容,你可以当成一篇涛涛雄辩的推理作品读。两百年后,依然能感受到萨迪文字中的澎湃激情与锋利洞见,这难道不比教科书鲜活?
两百年后的今天,目力所及依然没有找到这本小册子的完整中译本,作为一个14亿人口的泱泱大国,理解科学发展的方式和细节是一块重要拼图,其重要性不亚于科学结论。限于本人暂时法语水平有限,翻译只能做到从英译本到中译本,等时机成熟会从法语直译。
让上帝的归上帝,凯撒的归凯撒。这个中译本,纪念萨迪·卡诺,他天才的直觉和想象力,和他流星般激荡的一生。
正文 - Sadi Carnot 1824
论火的动力
所有人都知道热量可以产生运动。如今蒸汽机在各个地方都为人熟知,无人再会怀疑热中蕴含着庞大的力量。
热也是地球上发生的各种巨大运动的起因。它引起大气震荡,云朵上升,雨水降落和流星陨落,水流在地表切割出河道,它的力量被人类利用已久,但也只利用了其中很小一部分。甚至地震和火山喷发都是热的力量。
从这个庞大的储藏中,我们可以提取到必要的动力然后为我所用。大自然,从四面八方为我们提供了燃料,给了我们在任何地方和任何时间都能进行生产的力量,这就是热和它所产生的推动力。对这种动力进行开发,让其为我们所用,就是热机(heat engine)的目的。
对这类引擎(engine)的研究引起了极大的关注,它们的重要性无与伦比,对它们的使用与日俱增,以至于它们看起来就要在文明世界中引发一场巨大的革命。
如今,蒸汽机(steam-engine)已经在运转我们的矿场,推进我们的轮船,开掘我们的港口和河道,锻造钢铁,加工木材,碾碎谷物,纺纱编织我们的衣物,运输最沉重的物品,等等。它看起来一定会在将来的某天,变成一台普遍适用(universal)的发动机(motor),替代牲口,瀑布和气流的力量。
相比早期的引擎,这种发动机的第一个优势是更加经济高效,剩下两个无法估算的优势是它可以在所有时间和所有地点都能被不间断的使用。
如果某一天,蒸汽机可以如此完美,以至于用很低成本的燃料就能装配使用,那它就能结合所有吸引人的品质,然后让那些只能被隐约估计但范围极大的工业技术都能支付得起。它不仅仅是一个强劲且方便的发动机,它易于获取、能被携带到任何地方,它可以完全代替那台在用的机器,它甚至可以引发已有技术的快速延展、甚至创造全新的技术。
蒸汽机对英国最具标志性的公共服务业产生的影响,毫无疑问是对煤炭业的复兴,由于排水和提取煤炭的难度持续上升,英国的煤炭业一度下滑,甚至面临被迫中止的威胁。我们把蒸汽机对钢铁冶炼带来的收益排在第二位,因为丰富的煤炭储量替代了开始稀缺的木材供给,同时因为使用了蒸汽机允许或协助产生了那些强劲的机器。
钢铁和热量,如我们所知,是机械技术的支撑和基础。甚至可以说在英格兰,不存在任何一个工业行当可以不依赖或不自由使用这些原动力。夺走英格兰的蒸汽机就同时夺走了她的煤炭和钢铁。这就如同抽干她所有财富的源头,毁掉她繁荣赖以生存的基石,灭绝她一切庞大的力量。彻底摧毁她最强大的海军防御,可能都没有夺走她的蒸汽机这么致命。
能安全且快捷航行的蒸汽轮船,是因为蒸汽机才可能出现的全新技术。这种技术已经允许我们打造一个可以穿越大海和新旧大陆上各种河流的快速且频繁的通勤能力。它让我们穿越过去只能极为偶尔才能穿透的、最蛮荒的地区。它让我们携带文明的种子去往地球上曾经需要数年才能期待到达的地方。蒸汽航行让最遥远的国家变得近若比邻。它正把地球上的所有国家变成同一个国家的居民。事实上,减少旅行的时间、疲惫、不确定性和危险——不就正是在极大地缩短距离?
如同大多数人类发明,蒸汽机从诞生之初,就归功于不同人直接大胆的尝试,即使真正的发明者已无法确切知道。然而,在后续把蒸汽机改良成我们今天看到的样子中所包含的那些大胆尝试,比早期发明它的那些尝试,还要多得多。第一台装置中展现的蒸汽的辽阔力量和今天的蒸汽机相比,这中间的巨大差距,就好比人类的第一个竹筏和现代轮船的差距一般。
如果这项发现的荣耀属于那个通过这台机器获得了所有增长和发展的那个国家,那么这份荣耀不可避免地属于英格兰了。塞维利(Thomas Savery)、纽可门(Thomas Newcomen)、斯密顿(John Smeaton),还有著名的瓦特(James Watt)、伍尔夫(Arthur Woolf)、特里维西克(Richard Trevithick),和其他一些英格兰的工程师们,他们是蒸汽机名副其实的缔造者。他们通过双手推动了后面一系列的改良。最后,自然而然地,这个发明物在它最能强烈感受到被需要的地方,不断被发展、被完善。
尽管蒸汽机已经完成了各种各样的工作,尽管今天它所成就的状态令人满意,但关于这些机器的理论人们依旧知之甚少,改良它们的尝试仍然几乎完全取决于运气。
经常被提出的那个问题就是,热的动力是否是无穷的,对蒸汽机的改良是否有一个确定的限度——这个限度是指,自然事物无论如何都不允许超越的;或者,相反地,是否对其的改良可以无限地进行下去。我们长久以来都在思索,直到今天,我们都还在查明是否存在一种介质,比水蒸气更适合开发热产生的动力;还比如,是否空气真的在这种情况下就更不适合作此用途。我们现在提出这些问题,然后对其进行仔细考察。
热产生动力的现象还没有被从一般性的角度充分思考过。我们仅仅从机器的角度考量过,但这类机器由于使用中的性质和运动模式易受干扰,我们无法充分使用它们的全部潜力。所以这类机器中,热产生动力的现象,在一定程度上是不完整的。因此,识别那些基本原则或研究那些定律,就变得很困难。
为了研究最普遍意义上热生成动力的原理,这个原则的研究必须独立于机械构造或介质。无论机器的工作物质是什么,也不论运作方式是什么,有必要建立起一套原理,这个原理不仅适用于蒸汽机,也适用于所有假设的热机。
那些不从热量中接受动力的机器,它们动力来源于人或动物,瀑布,气流,等等,这些机器最微小的细节都可以用机械理论(mechanical theory)去研究。所有的情况都可以被预见,所有假象的运动模式都可以参考这些被严格地提出、且在任何状况下都可以使用的普遍法则。这是一个完整理论拥有的基本特征。很明显,对于热机也需要一套类似的理论。我们拥有的这套理论应该让物理法则得到足够的拓展延伸,足够的概括,能让热量在任何一个物体上的运行效果,可以被一种决定性的方式被提前预知。
我们假设接下来这部分是有关组成蒸汽机的各部件的浅显知识;同时我们认为不必再解释什么是锅炉(furnace)、汽锅(boiler)、汽缸(steam-cylinder)、活塞(piston)、冷凝器(condenser)、等等。
我们应该把注意力聚焦在蒸汽机中伴随动力产生的一个现象上。这个现象就是热质(caloric)的重新平等(re-establishing);那就是,热质从一个温度较高的物体,流向另一个温度较低的物体。一个运转的蒸汽机里,事实上到底发生了什么?锅炉中通过燃烧产生的热质,穿透汽锅的炉壁,产生蒸汽,通过某种方式与蒸汽合为一体。热质的重新平衡,即使不是全部,也至少部分发生在两方面。一方面,锅炉中的热空气围绕汽锅周边通过,在执行完它的功能后,以比从燃烧时获得的温度低得多的温度,从烟囱里排走;另一方面,冷凝器中的水,在液化了水蒸气后,以比进入机器时更高的温度排出。
动力因为蒸汽机而产生,并不是在于对热质的真实假设,而是在于热质从一个更热的物体流向一个更冷的物体的传导过程,也就是,关于这个热质平衡的重建——无论这种平衡是由于任何原因被打破了,比如被燃烧之类的化学行为,还是因为其他任何原因。我们很快会看到这个原则应用在被热驱动的任何机器上。
根据这个原则,仅仅产生热量是不足以产生动力的;冷源(cold)也是必须的;没有冷源,热量也毫无用处。事实上,如果我们发现物体和锅炉一样热,那我们该如何压缩蒸汽呢?产生的蒸汽能拿来干什么呢?我们不该假设我们可以把蒸汽排进大气里,虽然有些蒸汽机就是这么做的,但大气可能不会接受这部分蒸汽。在某些特定状况下它确实会接受这些蒸汽,因为大气满足了一个巨大冷凝器的空间,同时还因为它的温度更低;如果不是这样,那么它就会很快被充满,或者很快过饱和。
任何有温度差的地方,任何能让热质平衡被重新建立的地方,都有可能产生驱动力。蒸汽是实现这些动力的一种手段,但不是唯一的一种。所有自然物质都可以被作此用途,通过冷热交替,它们都容许体积变化,和一系列的收缩和膨胀。它们都可以在体积变化的过程中克服一定的阻力,也因此就能产生驱动力。固体——比如一根铁棒——长度在冷热交替中减少和增加,就可以移动绑在它们端部的物体。冷热交替中的液体可以减少和增加它的体积,它能在膨胀的相反方向上,克服或大或小的障碍物。气流体在温度变化下会有相当大的体积变化。如果它被封闭在一个可扩张的空间里,比如一个带有活塞的汽缸中,那么它就会在极大范围内提供运动。任何物质的蒸汽只要能转化为气体状态,比如酒精,水银,硫磺,等等,都可以满足水蒸气提供的相同用途。后者,在往复的加热和冷却中,能以永久气体的形态提供动力,也就是,永远不用变回液态。大多数这类设想的物质,很多都被试验过了,虽然到现在为止没有任何客观的成就。
我们已经说明了在蒸汽机中动力的产生源于热质平衡的再建立;这个过程不仅发生在蒸汽机中,还发生在所有的热机中——也就是说,对所有把热质作为动力源的机器当中。热量仅仅通过能让物体的体积和形状发生变化这一优点,就显而易见得可以作为动力的起因。
这些变化不是因为温度相同而引起的,而是由于交替地加热和冷却引起。加热任何一种物质都需要一个比被加热物体更热的物体;冷却也需要一个更冷的物体。我们可以给第一个物体提供热质,然后用这个中间物质中转传导给第二个物体。这就是重建,或至少努力去重建热质平衡的过程。
所以我们自然而然就会问出这个令人好奇且重要的问题:热的动力是否在数量上是恒定的,或这个数量是否随着被选作热行为的载体而作为中间物质去产生动力的介质的不同,而不同?
很明显这个问题只有在已知热质的数量,和已知温度差的情况下才能被问及。比方,我们假设一个物体A温度100°,另一个物体温度0°,然后问从第一个物体传导这么多热质(比如,和融化一千克的冰所需同样多的热质)到到第二个物体,能产生多大数量的动力。我们探究的是是否这个数量的限制是必须恒定,这个数量是否随着使用物质的变化而变化,是否水蒸气相比酒精、水银的蒸汽,永久气体,或任何其他物质,提供了更多或更少的优势。我们会利用已建立的一些猜想,来回答这些问题。
我们已经讨论过这个不证自明的事实,至少在一定程度上是不证自明的,只要我们开始思考因为热量引发的体积变化:无论任何地方,只要存在温度差,动力都可以被产生。相应地,任何能使用这种动力的地方,都可能被用来制造温度差,造成热质平衡被打破是可能的。物体的撞击和摩擦不正是真实地提升温度的方法吗,它们使物体可以自发达到比周围物体高的温度,从而引起了热质平衡被破坏,而这个平衡是之前存在的。根据经验得出的事实是,气态流体的温度可以因为压缩而上升或膨胀而下降。这是一种确定的可改变物体温度的方法,同时破坏这种物质的热质平衡多少次都可以。以水蒸气在蒸汽机中被利用的相反方式也可以被认为是破坏热质的方式。为了明确这一点,我们需要仔细观察水蒸气是如何开发热的动力的。试想有这样两个物体A和B,每个都保持恒定温度,A的温度比B的高。这两个物体,我们可以从中获取或移走热量而不改变物体的温度,它们可以被认为储存了无穷的热质。我们把第一个称作锅炉(Furnace),第二个称作冷却机(Refrigerator)。
如果我们希望把一定热量从A移动到B从而产生几动力,我们应该通过如下步骤进行操作:
(1)从物体A中获取热质产生蒸汽——也就是让A物体充当锅炉的角色,或是普通锅炉中组成汽锅(Boiler)的金属——我们假设产生的蒸汽和物体A的温度一样
(2)蒸汽被吸收进一个可伸缩的空间,比如一个安装有活塞的气缸中,可以增加空间以及气体的体积。因此气体变得稀疏后,温度自然而然就下降了,和所有弹性流体发生的现象一致;蒸汽的膨胀可以一直发生直到它完全达到物体B的温度。
(3)通过让蒸汽接触物体B将蒸汽冷凝,同时施加一个恒定的压力直到它完全液化。物体B在这里起到了一个普通引擎里冷凝水(Injection-water)的作用,但有一个区别,它把蒸汽冷凝的过程不与之混合,同时也不改变自身的温度。
我们刚刚描述的这个操作过程可以用相反的方向和顺序执行。完全可以通过物体B的热质产生蒸汽,当蒸汽与物体B的温度相当,压缩蒸汽直到它能开始吸收物体A的温度,最后让蒸汽和物体A接触凝结,直到被压缩至完全液化。
我们刚刚描述的这个操作过程可以用相反的方向和顺序执行。完全可以通过物体B的热质产生蒸汽,当蒸汽与物体B的温度相当,压缩蒸汽直到它能开始吸收物体A的温度,最后让蒸汽和物体A接触凝结,直到被压缩至完全液化。
通过我们的第一种操作,从物体A到物体B同时产生了动力和热质的传递。通过反向操作,过程中为了把物体B的热质还给物体A,也同时会消耗动力。但如果我们在每种状况下都在等量的蒸汽上操作,如果产生的动力和热质没有损耗,那么第一次产生的动力就和第二次产生的同样多,同时第一种情况下从物体A传导到物体B的热质,也就和第二次从物体B传导回物体A的热质一样多;于是一个无穷次的这类交替操作就可以被实施,最后从一个物体到另一个既没有产生动力,也没有传递热质。
现在假设如果存在一种比我们刚才使用的方式更好地利用热的方式,就是说,如果存在任何可能的方法,能让热质产生的动力比我们在第一次操作中产生的多一些,那么就足够把这些多出来的一部分动力,按照我们之前描述的方法,从冷源(refrigerator)物体B返回给热源(furnace)物体A,来重建一开始的状态,因此就能准备好让之前一模一样的操作再一次发生:这不仅仅是一种永恒动力,而且是在不消耗热质或其他任何介质的情况下产生无限动力。这样产生动力完全违背了被广泛接受的机械定律和可靠的物理原则。这是不可接受的。因此我们可以总结出,使用蒸汽能够产生的最大动力,就是利用任何其他介质能实现的最大动力。我们很快会给出第二种更严格的理论证明。上述过程只是一种近似。(参考59页)
对于我们刚刚阐述的命题,我们有权问这样一个问题:最大这个词语到底意味着什么?什么样的迹象标志着最大已经被实现了?通过什么样的迹象我们才能知道蒸汽是否已被用来开发了可能的最大动力?
因为每一次重建热质平衡的过程都是动力被产生的起因,每一次重建平衡的实现过程中没有用于产生动力的部分就应该被视为一种实际的损失。现在,几乎没有任何研究表明指出了不是由物体体积的变化引起温度变化都是无用的热质平衡。最大的必要条件就是,在物体中,被用来实现热的动力时,如果没有引发体积变化,那就不应发生任何温度变化。相应地,每一次发生这种情况那么最大的动力都可以被实现。这个原则绝不应该在制造热机(Heat Engine)的过程中被忽视;这是最根本的准则。如果这个标准不能被严格观测到,那么也应该尽可能少地偏离它。
每一个不是因为体积变化或化学反应引发的温度变化(一个我们在这里专门假设不应发生的情况),都是因为热质从一个或多或少更热的物体直接传递到一个更冷的物体。这种传递主要发生于不同温度物体的直接接触;因此这样的接触应该被尽可能地完全避免。这种接触不能被完全避免,但至少可以让相互接触的物体温差尽可能地小。当我们刚刚假设,在我们的说明中,物体A的热质被用来产生蒸汽,蒸汽被认为和物体A的温度一致;因此接触只发生在温蒂一直的物体上;之后发生的温度变化是因为膨胀,然后体积发生了变化。最后,冷凝(condensation)发生的时候不同温度的物体之间也没有发生接触。这个过程中蒸汽和与其温度相同的物体B接触,被施加了恒定的压力。因此,最大的条件被满足了。在现实中,这个过程不可能像我们假设的一模一样。为了决定热质从一个物体传递到另一个物体的,有必要假设一开始存在一点过量的温度,但是我们希望这种过量应尽可能地少。理论上我们认为这个量几乎不可察觉,因此不用损害我们论证的准确性。
针对我们的证明,一个很有价值的反对意见是:当我们从物体A获得热质来产生蒸汽,当蒸汽之后和物体B的接触中冷凝,用来产生这些蒸汽的水,我们认为一开始和物体A的温度一样,在操作过程的最后和物体B的温度一样。它变得温度更低了。如果我们希望和第一次一样再进行一番操作,如果我们希望利用这些工具开发出等量的动力,使用同样的蒸汽,那么第一步就是重建原有的状态——把水恢复到原来的温度。毫无疑问,这个可以通过让它接触物体A的方式完成;但是这就出现了两个不同温度的物体接触的状况,动力被损失了。于是我们不可能执行相反的操作,也就是,把物体A用来给液体升温的热质重新还回去。
这点困难可以被假设物体A和物体B之间的温差无限小来消除。用来把液体加热到之前温度的那部分热量同时也变得无穷小,并且和用来产生蒸汽的那部分热量——一个永远有限的量,相比可以忽略不计。
上述证明中两个物体的温度差无限小的假定,可以被轻松地推广至普遍情形。事实上,如果通过操作物体A把热质传递给物体Z来产生动力,那么后面这个物体的温度就是前一个物体差异极大,我们应该想象一系列物体B,C,D…的温度介于物体A,Z之间,然后使得A到B,B到C,等等,全部都是无穷小。来自A的热质在传递到Z之前,必须经过B,C,D,等等,然后每个阶段的传递都开发出了最大的动力。这个过程的反向操作也完全有可能,然后第52页的推断也可严格地被实现。
根据现在已经建立起来的原则,我们可以使用足够的精确性来把热的动力类比成落水瀑布。两种形式都有我们不可逾越的最大极限,一方面,无论是被水力驱动的任何机器,另一方面,无论是被热量驱动的任何物质。瀑布的动力取决于它的高度和流体的量;热的动力也取决于使用热质的数量,对其应称为,事实上我们也确实会叫做,落差(height of its fall),其含义是指,热质发生交换的物体间的温度差。瀑布产生的动力和高低水库间的高度差准确地成比例。热质降落所产生的动力毫无疑问随着冷热物体温度差异的增大而增大;但我们不知道动力是否和温差成比例。例如,我们就不知道,从100度到50度所流失的热质是否和50度到0度流失的热质所产生的的动力一样多。因此,这就是我们建议探究的问题。
在此,我们要对在第56页就清晰阐明的基本假设,给出第二个证明,然后把这个假定呈现为比刚给出的那个更普遍的形式。
但一种气态流体快速地被压缩,它的温度会升高。当它快速膨胀时,温度会下降。这个事实可以被实验最好地验证。我们将其作为证明的基础。
如果,当气体温度因为压缩而提升,而我们希望不施加体积变化而将它的温度降到之前,那它的一部分热质就需要被移除。我们可能通过移除与施加压力成比例的那么多热质,这样气体的温度就可以恒定在之前的水平。相似地,如果气体被舒张(rarefication),我们也可以通过增加一定量热质的方式避免其温度下降。让我们称这些没有温度变化时被施加的热质为,体积变化引起的热质。这种命名并不是表示热质涉及了体积变化:它也没有表明热质涉及了任何压力变化,但我们说压力变化引起的热质。我们不知道相较于体积变化时它遵循什么定理:它的数量变化很可能与气体的自然性质、密度和温度有关。实验在这一问题上没有告诉我们任何东西。它只是向我们表明,在压缩弹性流体(elastic fluid)时会或多或少地产生热质。
这个初步的观点建立之后,让我们想象一种弹性流体,比如空气,被封闭在一个圆柱型的容器(cylindrical vessel)中,abcd (Fig. 1),里面装着一个可运动的隔膜或活塞(piston),cd。让这里面有两个物体,A和B,每个都有温度恒定,A的温度比B高。让我们想象一个景象,如下描述的一系列操作:
(1)物体A接触封闭在空间abcd中的空气,或是这个空间的壁——这个壁我们假设可以完全及时地传递热质。通过接触,空气和物体A的温度变为相同;cd是活塞的实际位置。
(2)活塞逐渐上移到ef的位置。过程里空气和物体A始终接触,因此空气在舒张过程中一直保持恒温。物体A一直提供保持恒温所需的那部分热量。
(3)物体A被移除,于是空气不再与能够提供热质的物体接触。与此同时,活塞继续移动,越过ef的位来到gh。空气在没有获取热质的情况下舒张,它的温度也在下降。让我们想象它下降到和物体B一样的温度;这时候活塞立即停止运动,停止在gh的位置。
(4)让空气和物体B接触;空气这时候被压缩,活塞从gh返回到cd的位置。然而,空气始终保持恒温,因为它与物体B接触,可以把热质释放出给物体B。
(5)物体B被移除,空气的压缩继续进行,因为处于完全隔绝,空气的温度上升。压缩持续进行,直到空气到达物体A的温度。这时候活塞的位置从cd来到ik。
(6)空气再一次和物体A接触。活塞从ik的位置返回到ef;温度保持不变。
(7)步骤3描述过程再一次发生,然后依次是步骤4,5,7,3,4,6,3,5;一直持续。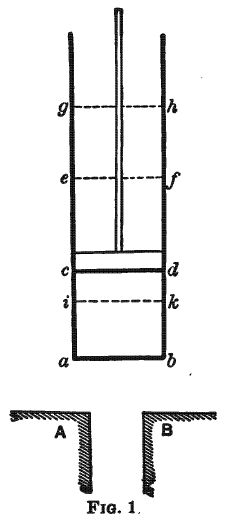
在这几个步骤中,活塞都在或多或少的程度上被封闭在施加影响;空气变化的弹性力很大程度上来源于体积变化和温度变化。但是需要注意的是,在同样的体积下,也就是活塞在同样的位置,扩张运动时的温度比收缩运动的温度高。在前一个状态下,空气的弹性力更大,因此扩张时产生的动力比收缩时产生的要更加可观。因此我们应该获取多余的动力——一种我们可以运用在任何目的上的多余动力。因此,空气已经被用来服务热机(heat-engine);实际上,我们已经以可能的最有利方式开发了它,因为没有无用的平衡重建影响到热质。
上述的这些过程都可以以相反的方式和顺序执行。让我们想象,在第六个环节之后,活塞的位置停在ef,我们使得活塞回到ik,与此同时我们让空气和物体A接触。这个物体在第六步中提供的热质会重新返回给它,也就是说,对于物体A,这时的情况和第五步结束的时候一模一样。如果现在我们拿走物体A,如果我们使得活塞从ef到cd,空气温度会降低在第五步中所升高的温度一样,最后就和物体B的温度一样。无疑我们还可以继续进行一系列的操作来逆转之所描述的步骤。而相应地,在相同情况下操作,有必要把扩张运动变为压缩运动。
第一类操作的结果是产生了一定量的动力,同时把物体A的热质移动到物体B。反向操作的结果是消耗所产生的动力同时把物体B的热质还给物体A;所以这两个系列的操作,以一种中和另一种的方式,相互抵消。
不可能让热质产生比我们在第一类操作中获得的动力更多的动力,现在就可以被轻易证明。这个证明过程和第56页中用到的推理非常相似;现在推理会变得更加明确。我们用来开发动力的空气,在每种循环操作结束时都被恢复成一开始就看到的原状,但是,正如我们已经讨论过的,这不仅仅只是针对水蒸气而言。
我们选择了气态空气作为开发动力的工具,但很明显这个推断对于所有气态物质都是一样的,甚至对于在收缩和膨胀中会易产生温度变化的物质都是成立的,这就包含了所有的自然物质,或者至少对那些适合开发动力的物质均是如此。因粗,我们可以引出这个普遍性的观点:
实现热的动力的过程是独立于工质(agents)存在的;热产生的动力数量只和受影响的、最后传递热质的物体间的温度所影响。
这里我们必须要理解,所有用来开发动力的方法都必须达到这个方法可到达的完美状态。这个状态只有在除了体积变化引发的温度变化外,没有别的任何温度变化,或者换句话说,如果没有发生不同温度的物体的直接接触,这个状态才能被满足。
不同的方式都可以实现热的动力,比如使用不同的物质,或者使用同种物质的两种不同状态——例如,同种气体的两种不同密度。
这就自然引导我们关注那些气态流体的有趣研究——这些研究向我们展现了关于热动力的新结果,同时在某些特殊的情况下,给了我们验证上述基础观点的手段。
我们已经看到,我们的证明可以被假设物体A和B的温差很小而简化。所以在步骤3和5的活塞活动也相当微小,这两个步骤可以在对产生动力几乎无影响的情况下被削减。非常小的体积变化足够产生足够小的温度差,然后这个足够小的体积变化在步骤4和6的存在下可以忽略不计,因为步骤4和6的大小可以是无限的。
如果我们在上述步骤中削减3和5,那么就会减少到如下:
(1)使密闭在abcd空间中的气体接触物体A(图2),活塞从cd移动到ef。
(2)移走物体A,使得密闭在abef中的气体接触物体B,活塞从ef回到cd。
(3)移除物体B,使得气体接触物体A,活塞从cd移动到ef,也就是重复第一阶段,以此往复。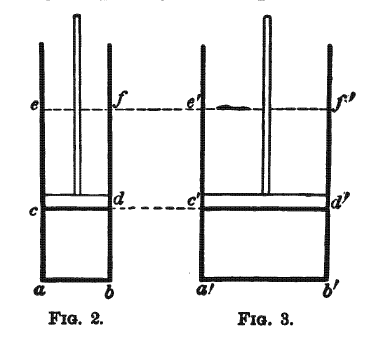
从1和2的整套操作中产生的动力很明显来自于两个温度之差,一个是使气体扩张时物体A的温度,另一个和使气体收缩时物体B的温度。
让我们假设操作1和2施加于两种不同化学构成但压强相等的气体——比如,都处于大气压强。这两种气体在相同状态的行为是一致的,也就是说,它们膨胀所产生的力,刚开始一样大,且会保持永远相等,无论体积和温度怎么变化,两者所提供的变化都是相同的。这很明显可以从Mariotte和MM. GayLussac以及Dalton的定理中推导出来——这个定理对所有弹性流体都适用,而且实质上这种体积,扩张力和温度之间的相同关系存在于所有弹性流体之中。
因为两种不同气体在相同的温度和相同的压强在相同的条件下表现的行为应该是一样的,如果让它们都处于上述的操作中,它们应该产生出等量的动力。
现在这就表明,基于我们建立的基本观点,两个操作中的热质是等量的;也就是说,无论是使用什么气体,从物体A传递给物体B的热质都是等量的。
很明显,从物体A传递到物体B的热质是气体在体积扩张中所吸收的,或是气体在收缩过程中所给出的。那么我们就可以建立其如下的假说:
当气体通过一个有限的体积和压强达到另一个同样有限的体积和压强时,所吸收和释放的热质永远是相等的,无论被选作实验对象的气体的自然属性如何。
比如,我们用大气压下100℃的1升空气。如果我们让空气体积加倍同时希望保持100℃的温度,那就必须给其补充一定量的热质。如果不使用空气,我们转而使用碳酸气体,氮气,氧气,氢气,水蒸气或酒精蒸汽,如果我们也把1升的这些气体体积加倍,同时置于大气压强下,所需的热质的量会和空气所需的完全一样。
反向操作也是一样的,如果不把体积加倍而是把体积减半,弹性流体所释放或吸收的热的数量从未被直接的实验观测过,毫无疑问这种实验是非常困难的,但有一个数据非常接近这个等价过程。支持它的是声学理论。因为状态的精确性这个论点很有说服力,如下:
大气压下的空气在突然经历体积压缩1/116时,温度会升高一度。
关于音速的实验实在760毫米汞柱的压强,温度6℃下,我们的数据只参考这两个条件。然而,为了更好的帮助我们,把温度定在0℃,基本是一样的。
空气压缩j1/116,因此温度上升1度,和空气直接被加热仅在密度上上升1度的是不同的。最开始的体积假设是V,压缩1/116把体积减少到V - 1/116V。
在恒定的压强下加热,根据M. Gay-Lussac定理,空气应该在0℃时增加1/267的体积:所以空气,一方面收缩时体积缩减到V - 1/116V;另一方面,膨胀时体积增加到V + 1/267V。
很明显在这两种不同状况下空气拥有的热量差,就是让其直接升温一度所需的那些热量;所以空气从体积为V - 1/116V膨胀到体积V + 1/267V所吸收的热量就是让温度上升一度所需的热量。
让我们现在假设,如果不允许空气子在受热自由膨胀时保持恒压,我们把气体封闭在一个体积不可变的空间中,在这种情况下我们使它的温度上升一度。to be continued...
Reflections On The Motive Power Of Heat And On Machines Fitted to Develop That Power
Dec 2022